Supplementary Angles: Explanation With Examples

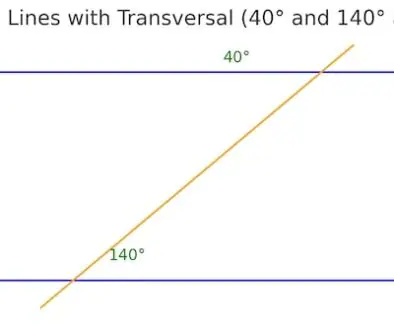
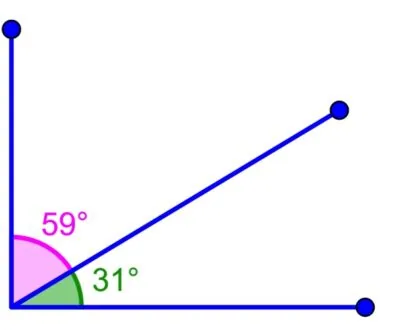
Supplementary angles refer to a pair of angles whose measures, when added together, sum up to 180 degrees. In other words, if the sum of two angles is 180 degrees, then they are supplementary angles.

For example, if one angle measures 60 degrees, then the other angle measures 120 degrees because 60 degrees + 120 degrees = 180 degrees. As a result, these two angles can be classified as supplementary angles.

Another example would be if one angle measures 75 degrees, then the other angle measures 105 degrees as well because 75 degrees + 105 degrees = 180 degrees. Hence, the pair of angles can be classified as supplementary angles.

Supplementary angles can be represented mathematically as follows: if angle A measures x degrees, then its supplementary angle B measures 180 – x degrees. For example, if angle A measures 60 degrees, then angle B measures 180 – 60 = 120 degrees.

Here are some example problems involving supplementary angles:

Find the measure of the supplementary angle to an angle measuring 70 degrees.
To find the supplementary angle, subtract the given angle from 180 degrees: 180 degrees – 70 degrees = 110 degrees. Therefore, the supplementary angle measures 110 degrees.

If one angle measures 100 degrees, what is the measure of its supplementary angle?
The supplementary angle measures 180 degrees – 100 degrees = 80 degrees. Therefore, the measure of the supplementary angle is 80 degrees.

Find the measure of each angle if they are supplementary and one angle measures 120 degrees.
Since the two angles are supplementary, we know that their measures add up to 180 degrees. Let us use x to represent the measure of the other angle. Then we can set up the equation:

120 degrees + x = 180 degrees

Solving for x, we get:

x = 180 degrees – 120 degrees

x = 60 degrees

Therefore, the other angle measures 60 degrees.

Supplementary angles are important in many mathematical applications, including geometry, trigonometry, and calculus. In geometry, complementary and supplementary angles are used to find the measures of missing angles in geometric figures, such as triangles and quadrilaterals. In trigonometry, supplementary angles are used to find the values of trigonometric functions, such as sine, cosine, and tangent.

In summary, supplementary angles are two angles whose measures add up to 180 degrees. They can be represented mathematically as 180 – x, where x is the measure of one of the angles. By understanding the concept of supplementary angles and how to calculate their measures, we can solve a variety of math problems involving angles and geometry.