Angle of Elevation – Definition, Example, and Video

The angle of elevation is a fundamental concept in mathematics that is used to calculate the height of an object based on the angle of elevation and the distance from the object. It is commonly used in geometry and trigonometry and has a wide range of applications in fields such as engineering, surveying, and physics.

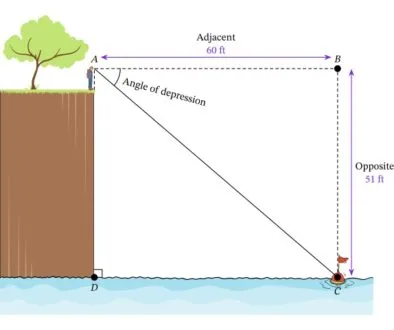
The angle of elevation is defined as the angle between a horizontal line of sight and the line from the observer’s eye to an object that is higher than the observer. To illustrate this concept, consider the following example:

Suppose you are standing at point A and looking at the top of a flagpole at point B. To calculate the angle of elevation, you need to draw a horizontal line from your eye to point C, which is directly below the flagpole. The angle of elevation is then the angle between the horizontal line and the line from your eye to the top of the flagpole.

To calculate the height of the flagpole, you need to use the trigonometric function tangent, which is defined as the ratio of the length of the opposite side to the length of the adjacent side. In this case, the opposite side is the height of the flagpole, and the adjacent side is the distance from your eye to point C.

Example: Let’s say that the distance from your eye to point C is 30 meters, and the angle of elevation is 30 degrees. Using trigonometry, we can calculate the height of the flagpole as follows:

tan(30 degrees) = height of flagpole / 30 meters

Solving for the height of the flagpole, we get:

height of flagpole = 30 meters x tan(30 degrees) = 17.32 meters (Because tan(30°) = 0.57735)

So the height of the flagpole is approximately 17.32 meters.

Another example of the angle of elevation is calculating the height of a hot air balloon. Suppose you are standing at point A and looking up at a hot air balloon at point B. To calculate the angle of elevation, you need to draw a horizontal line from your eye to point C, which is directly below the hot air balloon. The angle of elevation is then the angle between the horizontal line and the line from your eye to the bottom of the hot air balloon.

Suppose the distance from your eye to point C is 50 meters, and the angle of elevation is 60 degrees. Using trigonometry, we can calculate the height of the hot air balloon as follows:

tan(60 degrees) = height of hot air balloon / 50 meters

We can obtain the height of the hot air balloon by solving the equation:

height of hot air balloon = 50 meters x tan(60°) = 86.6 meters (Because tan(60°) = √3 = 1.732)

So the height of the hot air balloon is approximately 86.6 meters.

The angle of elevation has many practical applications, such as in surveying, where it is used to measure the height of buildings, trees, and other structures. It is also used in physics to calculate the trajectory of projectiles, such as missiles and rockets, and in engineering to design and build structures that are stable and secure.

In conclusion, the angle of elevation is a fundamental concept in mathematics that is used to calculate the height of an object based on the angle of elevation and the distance from the object. By understanding this concept and applying it to real-world situations, we can make accurate measurements and calculations that have a wide range of practical applications.