Learn Linear Pair of Angles: Defining With Examples
Before you go ahead and start banging your head that you don’t understand Linear Pair of Angles. Make sure you already know what are Adjacent Angles and Opposite Rays. You will never understand Linear Pair unless you understand Adjacent Angles and Opposite Rays. So make sure you learn them first and come back to this page to proceed.
What is Linear Pair of Angles?
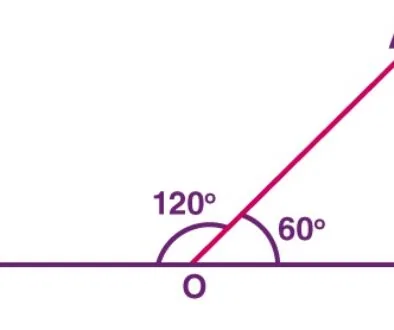
Definition: Linear Pair of Angles are those Adjacent Angles whose non-common sides form opposite rays.
Or you can define this way: Linear pair is the pair of 2 adjacent angles whose sum is 180 degrees, and they make opposite rays.
Example:
∠1 and ∠2 or ∠WZY and ∠XZY are adjacent angles and their non-common sides ZW and ZX are opposite rays. So ∠WZY (∠2) and ∠XZY (∠1) are forming a Linear Pair. The measure of these 2 angles will add up to 180 degrees.
Points to remember about Linear Pair:
- It is a pair of 2 Adjacent Angles
- The non-common sides are opposite rays
- The sum of the 2 angles will always be 180 degrees (Check the math section after this video)
- All Adjacents angles do not mean to form a Linear Pair.
Let’s learn to Identify Linear Pair in a better way with this video
The Math
Question: The angles ∠POR and ∠QOR makes a Liner Pair. If a – b = 40°, find the value of a and b .
Solution:
As we already said earlier while defining Linear Pair: If angles are forming a Linear Pair, the sum of both angles will always be 180°.
So, a + b = 180° —–(i)
We already know a – b = 40° —– (ii)

a = 220° / 2
a = 110°
Now we have the value of a .
So let’s get the value of b .
We know that:
a = 110°
a – b = 40°
| 110° – b = 40° b = 110° – 40° b = 70° |
So the answer is a = 110° and b = 70°
And if you add a+b, it will certainly be 180°