What Are Adjacent Angles? Explanation and Examples
What Are Adjacent Angles?
Adjacent Angles are those angles that share a common side and a common point (vertex) and they shouldn’t overlap. Let’s point the conditions.
Adjacent Angles are those:
- Have Common Vertex (Common Point)
- Have Common Side (Also known as Common Arm)
- Must not Overlap (They should not have a common interior point)
An Example of Adjacent Angles:
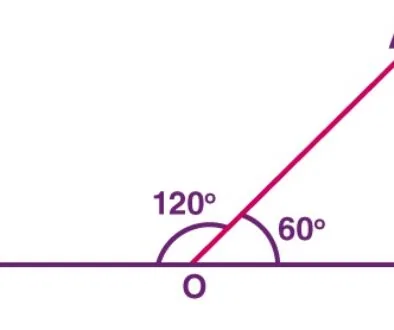
In the Example above, angle ∠DBC is adjacent to the angle ∠CBA. Therefore, ∠DBC and ∠CBA are Adjacent Angles.
Why ∠DBC and ∠CBA are Adjacent Angles
- ∠DBC and ∠CBA share the common vertex B (Common Point B)
- ∠DBC and ∠CBA have a common side BC
- They do not overlap (They do not have a common interior point). (See the question below that has the same image to learn more about this point)
The below image doesn’t make Adjacent Angles:

Explanation: The angles ∠FGH and ∠GHI are not adjacent angles because they do not have Vertex (a common point shared by both the angles).
Here is another example where Angles Do not make Adjacent Angles:

Explanation: ∠JNK and ∠LNM are not adjacent angles because they do not have a common side. However, ∠JNK and ∠KNL are adjacent angles because they have the common side (NK) and Vertex (N). In the same way, ∠KNL and ∠LNM are also adjacent angles because they share the common side (NL) and Vertex (N).
Question: Why the angles ∠DBC and ∠DBA are not adjacent angles?
Answer:
∠DBC and ∠DBA share a common interior point (C). In another word, C is the interior point in the middle of the ∠DBA angle. As we mentioned at the start the angles should not have a common interior point to be adjacent angles.
If it is still confused to you, take it this way: The other 2 sides must lie on the opposite side of the common side. If we take CB as the common side, DB and AB are on the opposite side of CB. So ∠DBC and ∠CBA do make the adjacent angles, but ∠DBC and ∠DBA do not make adjacent angles.