Angle of Depression – Learn With Definition and Examples

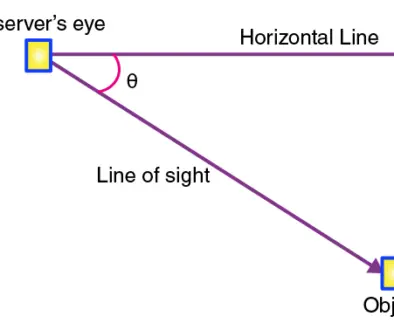
The angle of depression is a term used in mathematics and physics to describe the angle between a horizontal line and a line of sight that points downward. It is the opposite of the angle of elevation, which measures the angle between a horizontal line and a line of sight that points upward.

The angle of depression is important in many fields, such as surveying, engineering, and physics. It is used to calculate the height, distance, and position of objects that are below the observer’s line of sight. The angle of depression is typically measured in degrees or radians.

Here are two examples that illustrate the concept of the angle of depression:

Example 1: Suppose you are standing at the top of a building and looking down at a car on the street below. To calculate the angle of depression, you need to draw a line of sight from your eye to the car, and then draw a horizontal line from your eye to the ground. The angle of depression is then the angle between the horizontal line and the line of sight to the car.

Let’s say that the height of the building is 50 meters, and the angle of depression is 30 degrees. Using trigonometry, we can calculate the distance from the building to the car as follows:

** d = distance of car

tan(30°) = 50m / d

Where d represents the distance from the building to the car.

To solve for d, we can rearrange the equation:

d = 50m / tan(30°)

Now, substituting the value of tan(30°) as 1 / √3, we get:

d = 50m / (1 / √3)

Multiplying the numerator and denominator by √3, we get:

d = (50m x √3) / 1

Simplifying, we get:

d ≈ 86.6 meters

So the car is approximately 86.6 meters away from the building.

Example 2: Suppose a person standing on the edge of a cliff is looking down at a boat in the water below. The person measures the angle of depression to the boat as 45 degrees. If the height of the cliff is 100 meters, the person can use trigonometry to calculate the distance from the boat to the cliff. The person knows that the angle of depression is equal to the angle of elevation of the boat as seen from the water.

Let’s say the person estimates the distance from the cliff to the boat to be 200 meters. Using the tangent function, the person can solve for the height of the boat as follows:

** h = height of boat

tan(45°) = h / 200m

Where h represents the height of the boat.

To solve for h, we can rearrange the equation:

h = 200m x tan(45°)

Now, substituting the value of tan(45°) as 1, we get:

h = 200m x 1

Simplifying, we get:

h ≈ 200 meters

So the height of the boat above the water is approximately 200 meters.

In conclusion, the angle of depression is an important concept in mathematics and physics that is used to calculate the height, distance, and position of objects that are below the observer’s line of sight. It is an essential tool for engineers, surveyors, and scientists who need to measure and analyze the world around us. By understanding the principles of trigonometry and geometry, we can make accurate measurements and calculations that have a wide range of practical applications.