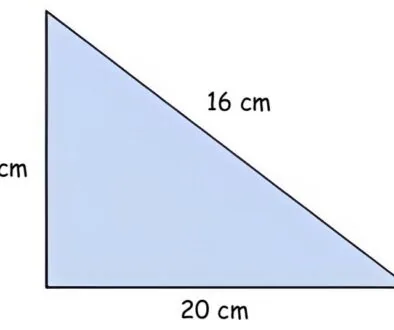
How to Find Missing Sides Value of Tringle
Finding the Missing Side Value of the Triangle with this calculator
How to Calculate Missing Sides
When you know the perimeter of a triangle and the lengths of two of its sides, you can use the formula:
Missing side = Perimeter – One known side – Another known side
to find the length of the missing side. This formula works for any type of triangle – equilateral, isosceles, or scalene.
To use the formula, you’ll need to know the length of two of the sides of the triangle. If you don’t know the length of any of the sides, this formula won’t be helpful. Once you have the values, you can simply substitute them into the formula and solve for the missing side.
Here are some examples to help illustrate the process:
Example 1

Finding the missing side of an isosceles triangle Suppose we have an isosceles triangle with a perimeter of 24 cm. We know that two sides are equal and one side is different, but we don’t know their length. Let’s say the length of one of the equal sides is 8 cm. To find the length of the missing side, we can use the formula above:
Since the length of all sides in an isosceles triangle is equal. So the other 2 sides will also be 8 cm. You don’t even need to calculate.
Missing sides = 8 cm and 8cm (So all 3 sides will be 8 cm)
Example 2

Finding the missing side of a scalene triangle Suppose we have a scalene triangle with a perimeter of 20 units. We know the length of one side is 7 units and another side is 5 units. To find the length of the missing side, we can use the formula:
Missing side = Perimeter – One known side – Another known side
Missing side = 20 – 7 – 5 Missing side = 8 units
Therefore, the length of the missing side of the scalene triangle is 8 units.
In conclusion, the formula Missing side = Perimeter – One known side – Another known side is a simple and effective way to find the missing side of a triangle. By knowing the perimeter and lengths of two other sides of a triangle, you can easily find the length of the missing side. This formula is especially useful in real-life situations involving geometry, engineering, and architecture.